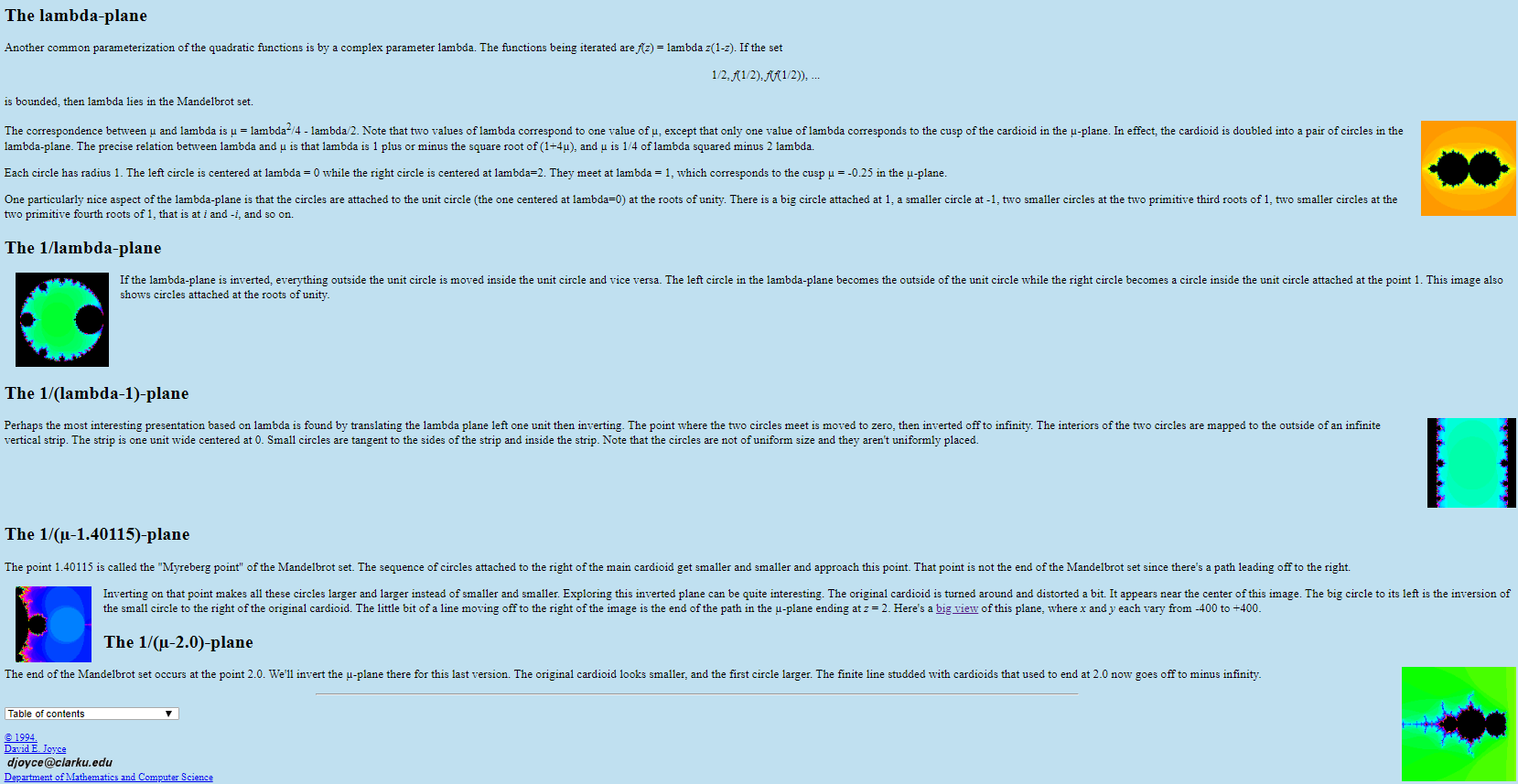
I've never seen this terminology before, but it looks like what XaoS calls a "plane" is what UF calls a "mapping" or "transformation". The "mu plane" is normal mode, no mapping. The "1/mu plane" is done in UF with the Inverse mapping. To get the "lambda plane", we need a lambda mapping in UF. I found one in the public formulas! In the Mapping tab, choose "Plug-In Transformation" from standard.uxf. Then for its Transformation, go to thm.ulb and choose "THMLambdaMapping". To get something like the lambda plane image shown in the first post, use Mandelbrot as the formula and set the THMLambdaMapping parameter factor(Re) to 2. For the 1/lambda-plane, also change fn(z2) to recip. I don't see a way to get the 1/(lambda-1) plane; you'd probably need to write a new transformation.
I've never seen this terminology before, but it looks like what XaoS calls a "plane" is what UF calls a "mapping" or "transformation". The "mu plane" is normal mode, no mapping. The "1/mu plane" is done in UF with the Inverse mapping. To get the "lambda plane", we need a lambda mapping in UF. I found one in the public formulas! In the Mapping tab, choose "Plug-In Transformation" from standard.uxf. Then for its Transformation, go to thm.ulb and choose "THMLambdaMapping". To get something like the lambda plane image shown in the first post, use Mandelbrot as the formula and set the THMLambdaMapping parameter factor(Re) to 2. For the 1/lambda-plane, also change fn(z2) to recip. I don't see a way to get the 1/(lambda-1) plane; you'd probably need to write a new transformation.