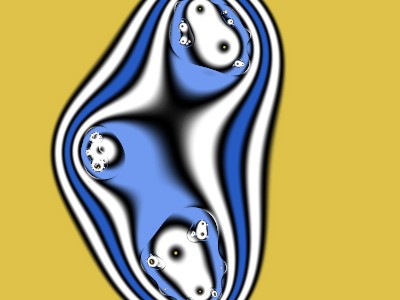
I’ll start with this quotation from the UF help file:
Since the first release of Ultra Fractal in 1998, the formulas written for it have become larger and more complex. Even though many formulas are quite similar, they could not share any common code, but had to be written as stand-alone formulas. For example, if you wanted to add just one new feature to an existing formula written by someone else, you had to create a new formula, duplicate all the code from the original formula, and only then add some new things.
To improve this situation, Ultra Fractal 5 introduced the ability for formulas to re-use common code via plug-ins. You can view a plug-in as a “black box” that adds functionality to a formula. Via plug-in parameters, a formula enables you to select the actual plug-in that performs an action for the formula.
The formula declares what kind of functionality it needs and you can select any compatible plug-in to actually implement it. This makes it possible for formula authors to write a new plug-in to implement just the new feature that they want to add to an existing formula. The formula doesn't have to be changed at all. You just select the new plug-in when you use the formula.
For everyday users, plug-ins make it possible to combine existing elements in new ways without needing to do any programming. For formula authors, plug-ins make it easier to write and manage complex formulas.
More than 15 years later, I have seen few users and formula authors take advantage of plug-ins. For example, on the excellent site https://www.deviantart.com/ultra-fractal-redux, many fractals are available along with their parameters but few of them use plug-ins.
Perhaps the reason for not using plug-ins is that formula writers have not written their formulas with sufficient flexibility. I have been working on flexible plug-in formulas since the early days of UF5, with many tries that I’ve since rejected (note the large number of “NotRecommended” lines in jlb.ulb). This tutorial covers the latest (though perhaps not the last) version.
This is a long tutorial and you don’t have to do it all at once. The images are meant only as illustrations, not for any artistic merit. Artistry is up to the user.
While writing about my programs, I realized that I needed to make many minor improvements. Therefore you’ll need to download the latest versions.
This tutorial only discusses plug-ins for the Formula tab. A later tutorial will discuss plug-ins for the Coloring/Outside tab.
Start with this upr:
1 {
::yCfy9gn2Vi1SzNKOQ47pq8fgi7TiAb8jZLdYcSlpqpmsXSSVezFKFQYrNCJWhYTc+1PNvsNg
4hvYb03X3q7mu/Q4IFJQT4f/6rss0MNnitdst+gFq3jXhQW7psd714FwP5kDUVK2xKQRDZ6U
s9vYxWb4Z0/y92V36icnbn7GiQzIcGJlJ2hPQTv+qCLL2iASimJFY7Nkg33pkZiQbLZCJgpP
gdgNJmq3LDxxZcNLhkCGHTSSAPVaOVopKM6WgIZnA7c9VRSFQmUAHT+klj76hsSoqg90g3xy
oIrIGnKIxQy9kmICJqwbyiiLiWwjqDY7fSFUFL4hSvZbl4X5474QUgt/X+b3kxf77/63b8f6
DmOYfh1Npdz/7vr0PF5SHwqLzBNZMUdzrNuzROOetR3TSfjw44/Jvg2x29yPw3zAPA7vuNYk
/mNNzgNIkpwPn4w5w95xgMT3TKcXNM6GEC50GeD0TEU2S0x0EFFLkGW9lnbGSmttglWREp5I
jwLLlqmG33ZiQ8PCDNjqPkQx/mJoEVveI75ml+Xe2/hMRQ+Ug9AGNxcOb6pd2ll5A9WROyLQ
mOYM/8wNPl8oO5zv96GqL084cbPGDzOGtNyvay98JcIurvw/R4bK/NlUbPk5jW2Pn5wjznzM
se0cqmkqJKdP1pTsS8Tkfkr3NKvhHbPycbz74Psdq1ttTvwtd6VutQk/YxQmZNjGETp0Qo74
bob8GjaZVbkq72WCyDz9o02QbcP3oSkpaTafwyTR8rm2oz11EnkIQJ5e1/KhHRAsk0lqAWb1
Uz8sLI5zuw8/SUBPZxUj8Spw+ArEC738CxwOYn3dzEpsQa5h7KSYAQIFUrUJnFin7uahnzMH
P3rvCUH6ylXcr9I7lrcnNL/ogmOPVA3w5p+piEygluTylK4UcVFugqLNc4q7Hiannv0Gt+6T
19O2XFRjys9pxaCXWSOKL1E8cxgmIhyImgw7zwoXf9U141XtNRwUzVTSExO4c8dLPRfh/6Lj
b7LjOi2xgxDjo+UlMRrnZyuUbFpuep/nq3YcKRZIDUfb2C6/0929ydiuEodP8FREQxuOOIn1
DQ9seNkT/8ChArVoicsHm/UD30ACnasntEPCePRpC71vHYCIPqeQWT8XSpPyEPS+EANZfYYM
DeZOTrD20TYnKjp+EOHbb9DOv7oS5RombyU4tliJiDG1QiCa1NcHyzcJOQPicU5o+fD6tmsv
6obdWv+oaG7XU0AWipSM8heHJNp/tz/IFoDrWFsQuPNWKhX3P/ePcOPSxLo76uyCe2P9T88Z
rtKcFe+yFrmv846LcqWv42T1irmVtozilLX6CKnlAeIPzAOwG1xNOwLwXxGeE1qZrR1ALd7B
Y98uux1Zp5N19YO1GwUS5eKp8WicXAGXCMDtoHATJ1sTJVzNd2pkqFwavuu5b1knva9aPPAp
6/P587lQHSJb0x/dFXPY29PAovBFHD==
}

The Formula tab uses “Plug-In Formula” from Standard.ufm, “Switch Formula” from jlb.ulb, and “Standard_Mandelbrot” from Standard.ulb. This shows the usual Mandelbrot Set, the red part (red is the “Solid Color” set on the Inside tab). Everything outside the red part diverges.
For the rest of this tutorial I won’t change the gradient or the coloring and will work with only one layer. Unless I say otherwise, I’ve used the default parameters
Switch Formula (SF) allows two types of formula plug-ins. If “Does Formula do its own bailout test?” is “Yes”, SF looks for formulas of the Formula class (defined in common.ulb), such as those in Standard.ulb, mt.ulb, and om.ulb. These use the bailout test defined in the Formula class and set their own “c” values. If the answer is “No”, SF looks for formulas of the FormulaX class, currently only found in jlb.ulb. SF handles bailout as well as setting the “c” value.
Experiment with Yes formulas and then set the answer to No. Make sure that the “Divergent bailout method” is set to “B00 |z|”, as this corresponds to the method used in Standard_Mandelbrot. The difference in the coloring is because Standard_Mandelbrot starts with z of 0 and SF starts with z equal to the pixel. (In SF, this can be changed; see later in this tutorial.)
The next line is “Bailout type”. SF allows this to be Divergent, Convergent, or Either. With Divergent, we see the usual Mandelbrot set. Set the Bailout type to Convergent.

The yellow area that’s inside the Mandelbrot set converges. (Yellow is the color at position zero of the gradient.) The outside seems to converge, but before we saw that it diverged. What happened? The outside pixels, given enough iterations, go to INF, a value too large for the computer to handle, so Ultra Fractal (UF) bails out. Change the “Periodicity Checking” to Normal. Note that UF’s periodicity checking can’t deal properly with much of the inside area.
Change the “Periodicity Checking” to Off and set the “Bailout type” to Divergent.
The next line down is “Divergent bailout method”. Click on that line’s Browser button and a browser pops up with thumbnails showing the effect of each of the 10 possible bailout methods. For this fractal they all look alike, but that’s not true for all fractals. Note: If you click on View, Preferences, Browser, you can change the size of the thumbnails that are shown. Mine are set to 200 by 150, larger than the default value.
The next line down is “Bailout value”. Here it’s set to 100. With z = x+iy, or (x,y), “B00 |z|” bails out when (x^2+y^2) is larger than 100. Similarly, “B04 |Real| and |Imag|” bails out when both abs(x) and abs(y) are larger than 10. Most users will just look at the thumbnails to decide which method to use.
Note that all FormulaX plug-ins can do both M-type, with c the pixel value, and “J-type”, with c the seed value. There’s no need to have two different plug-ins. Uncheck M-type to see a Julia fractal with the default seed of (1, -0.5).

Unchecking “Basic Mandelbrot” gives you the option to change the power from 2 to any complex number. That’s within the Mandelbrot plug-in.
Unchecking the “Basic version of Switch Formula” will unlock the advanced features of SF. For example, it’s possible to tweak z before the first iteration, and it’s possible to tweak z after each iteration. In each case this is done with the Tweak plug-in. (Tweak is probably an inaccurate name, as the plug-in can make a small change to z or completely change z.) Replacing the initial value of z with (0,0) will give the same coloring as with Standard_Mandelbrot.
Set the Mandelbrot plug-in to J-type, seed (1,-0.5), and check “Tweak z before first iteration?”. You have the option to “Add” something to z or to “Replace” z. You have the option of a simple linear expression or using a plug-in Transformation. Experiment. The default Transformation is “Function Transformation”, which has many plug-ins; you can see them as thumbnails if you click on the Browse button on the line below “Function Transformation”. Experiment. Here is the result for Replace, e1 = (0,0), e2 = (1,0), a = (1,0), and transformation “16 acotanh”.

Uncheck “Tweak z before first iteration?” and check “Tweak z after each iteration?”. Experiment. Here’s the result for Add, e1 = (-1,0), e2 = (0.2,0), a = (1,0), and transformation “27 log”.

[Continued as a Reply]
I’ll start with this quotation from the UF help file:
_Since the first release of Ultra Fractal in 1998, the formulas written for it have become larger and more complex. Even though many formulas are quite similar, they could not share any common code, but had to be written as stand-alone formulas. For example, if you wanted to add just one new feature to an existing formula written by someone else, you had to create a new formula, duplicate all the code from the original formula, and only then add some new things.
To improve this situation, Ultra Fractal 5 introduced the ability for formulas to re-use common code via plug-ins. You can view a plug-in as a “black box” that adds functionality to a formula. Via plug-in parameters, a formula enables you to select the actual plug-in that performs an action for the formula.
The formula declares what kind of functionality it needs and you can select any compatible plug-in to actually implement it. This makes it possible for formula authors to write a new plug-in to implement just the new feature that they want to add to an existing formula. The formula doesn't have to be changed at all. You just select the new plug-in when you use the formula.
For everyday users, plug-ins make it possible to combine existing elements in new ways without needing to do any programming. For formula authors, plug-ins make it easier to write and manage complex formulas._
More than 15 years later, I have seen few users and formula authors take advantage of plug-ins. For example, on the excellent site https://www.deviantart.com/ultra-fractal-redux, many fractals are available along with their parameters but few of them use plug-ins.
Perhaps the reason for not using plug-ins is that formula writers have not written their formulas with sufficient flexibility. I have been working on flexible plug-in formulas since the early days of UF5, with many tries that I’ve since rejected (note the large number of “NotRecommended” lines in jlb.ulb). This tutorial covers the latest (though perhaps not the last) version.
This is a long tutorial and you don’t have to do it all at once. The images are meant only as illustrations, not for any artistic merit. Artistry is up to the user.
While writing about my programs, I realized that I needed to make many minor improvements. Therefore you’ll need to download the latest versions.
This tutorial only discusses plug-ins for the Formula tab. A later tutorial will discuss plug-ins for the Coloring/Outside tab.
Start with this upr:
1 {
::yCfy9gn2Vi1SzNKOQ47pq8fgi7TiAb8jZLdYcSlpqpmsXSSVezFKFQYrNCJWhYTc+1PNvsNg
4hvYb03X3q7mu/Q4IFJQT4f/6rss0MNnitdst+gFq3jXhQW7psd714FwP5kDUVK2xKQRDZ6U
s9vYxWb4Z0/y92V36icnbn7GiQzIcGJlJ2hPQTv+qCLL2iASimJFY7Nkg33pkZiQbLZCJgpP
gdgNJmq3LDxxZcNLhkCGHTSSAPVaOVopKM6WgIZnA7c9VRSFQmUAHT+klj76hsSoqg90g3xy
oIrIGnKIxQy9kmICJqwbyiiLiWwjqDY7fSFUFL4hSvZbl4X5474QUgt/X+b3kxf77/63b8f6
DmOYfh1Npdz/7vr0PF5SHwqLzBNZMUdzrNuzROOetR3TSfjw44/Jvg2x29yPw3zAPA7vuNYk
/mNNzgNIkpwPn4w5w95xgMT3TKcXNM6GEC50GeD0TEU2S0x0EFFLkGW9lnbGSmttglWREp5I
jwLLlqmG33ZiQ8PCDNjqPkQx/mJoEVveI75ml+Xe2/hMRQ+Ug9AGNxcOb6pd2ll5A9WROyLQ
mOYM/8wNPl8oO5zv96GqL084cbPGDzOGtNyvay98JcIurvw/R4bK/NlUbPk5jW2Pn5wjznzM
se0cqmkqJKdP1pTsS8Tkfkr3NKvhHbPycbz74Psdq1ttTvwtd6VutQk/YxQmZNjGETp0Qo74
bob8GjaZVbkq72WCyDz9o02QbcP3oSkpaTafwyTR8rm2oz11EnkIQJ5e1/KhHRAsk0lqAWb1
Uz8sLI5zuw8/SUBPZxUj8Spw+ArEC738CxwOYn3dzEpsQa5h7KSYAQIFUrUJnFin7uahnzMH
P3rvCUH6ylXcr9I7lrcnNL/ogmOPVA3w5p+piEygluTylK4UcVFugqLNc4q7Hiannv0Gt+6T
19O2XFRjys9pxaCXWSOKL1E8cxgmIhyImgw7zwoXf9U141XtNRwUzVTSExO4c8dLPRfh/6Lj
b7LjOi2xgxDjo+UlMRrnZyuUbFpuep/nq3YcKRZIDUfb2C6/0929ydiuEodP8FREQxuOOIn1
DQ9seNkT/8ChArVoicsHm/UD30ACnasntEPCePRpC71vHYCIPqeQWT8XSpPyEPS+EANZfYYM
DeZOTrD20TYnKjp+EOHbb9DOv7oS5RombyU4tliJiDG1QiCa1NcHyzcJOQPicU5o+fD6tmsv
6obdWv+oaG7XU0AWipSM8heHJNp/tz/IFoDrWFsQuPNWKhX3P/ePcOPSxLo76uyCe2P9T88Z
rtKcFe+yFrmv846LcqWv42T1irmVtozilLX6CKnlAeIPzAOwG1xNOwLwXxGeE1qZrR1ALd7B
Y98uux1Zp5N19YO1GwUS5eKp8WicXAGXCMDtoHATJ1sTJVzNd2pkqFwavuu5b1knva9aPPAp
6/P587lQHSJb0x/dFXPY29PAovBFHD==
}

The Formula tab uses “Plug-In Formula” from Standard.ufm, “Switch Formula” from jlb.ulb, and “Standard_Mandelbrot” from Standard.ulb. This shows the usual Mandelbrot Set, the red part (red is the “Solid Color” set on the Inside tab). Everything outside the red part diverges.
For the rest of this tutorial I won’t change the gradient or the coloring and will work with only one layer. Unless I say otherwise, I’ve used the default parameters
Switch Formula (SF) allows two types of formula plug-ins. If “Does Formula do its own bailout test?” is “Yes”, SF looks for formulas of the Formula class (defined in common.ulb), such as those in Standard.ulb, mt.ulb, and om.ulb. These use the bailout test defined in the Formula class and set their own “c” values. If the answer is “No”, SF looks for formulas of the FormulaX class, currently only found in jlb.ulb. SF handles bailout as well as setting the “c” value.
Experiment with Yes formulas and then set the answer to No. Make sure that the “Divergent bailout method” is set to “B00 |z|”, as this corresponds to the method used in Standard_Mandelbrot. The difference in the coloring is because Standard_Mandelbrot starts with z of 0 and SF starts with z equal to the pixel. (In SF, this can be changed; see later in this tutorial.)
The next line is “Bailout type”. SF allows this to be Divergent, Convergent, or Either. With Divergent, we see the usual Mandelbrot set. Set the Bailout type to Convergent.

The yellow area that’s inside the Mandelbrot set converges. (Yellow is the color at position zero of the gradient.) The outside seems to converge, but before we saw that it diverged. What happened? The outside pixels, given enough iterations, go to INF, a value too large for the computer to handle, so Ultra Fractal (UF) bails out. Change the “Periodicity Checking” to Normal. Note that UF’s periodicity checking can’t deal properly with much of the inside area.
Change the “Periodicity Checking” to Off and set the “Bailout type” to Divergent.
The next line down is “Divergent bailout method”. Click on that line’s Browser button and a browser pops up with thumbnails showing the effect of each of the 10 possible bailout methods. For this fractal they all look alike, but that’s not true for all fractals. Note: If you click on View, Preferences, Browser, you can change the size of the thumbnails that are shown. Mine are set to 200 by 150, larger than the default value.
The next line down is “Bailout value”. Here it’s set to 100. With z = x+iy, or (x,y), “B00 |z|” bails out when (x^2+y^2) is larger than 100. Similarly, “B04 |Real| and |Imag|” bails out when both abs(x) and abs(y) are larger than 10. Most users will just look at the thumbnails to decide which method to use.
Note that all FormulaX plug-ins can do both M-type, with c the pixel value, and “J-type”, with c the seed value. There’s no need to have two different plug-ins. Uncheck M-type to see a Julia fractal with the default seed of (1, -0.5).

Unchecking “Basic Mandelbrot” gives you the option to change the power from 2 to any complex number. That’s within the Mandelbrot plug-in.
Unchecking the “Basic version of Switch Formula” will unlock the advanced features of SF. For example, it’s possible to tweak z before the first iteration, and it’s possible to tweak z after each iteration. In each case this is done with the Tweak plug-in. (Tweak is probably an inaccurate name, as the plug-in can make a small change to z or completely change z.) Replacing the initial value of z with (0,0) will give the same coloring as with Standard_Mandelbrot.
Set the Mandelbrot plug-in to J-type, seed (1,-0.5), and check “Tweak z before first iteration?”. You have the option to “Add” something to z or to “Replace” z. You have the option of a simple linear expression or using a plug-in Transformation. Experiment. The default Transformation is “Function Transformation”, which has many plug-ins; you can see them as thumbnails if you click on the Browse button on the line below “Function Transformation”. Experiment. Here is the result for Replace, e1 = (0,0), e2 = (1,0), a = (1,0), and transformation “16 acotanh”.

Uncheck “Tweak z before first iteration?” and check “Tweak z after each iteration?”. Experiment. Here’s the result for Add, e1 = (-1,0), e2 = (0.2,0), a = (1,0), and transformation “27 log”.

[Continued as a Reply]