Hello,
I have been working with a formula for a while, which I have been calling Mandalamandelbrot and Mandaljulia, because it creates nice patters with circular symmetries depending on the location and parameters used. Here are a few examples:
https://www.deviantart.com/rychveldir/art/Almond-Ship-931583199
https://www.deviantart.com/rychveldir/art/Mandala-Chain-912805646
https://www.deviantart.com/rychveldir/art/Green-Stars-904525576
https://www.deviantart.com/rychveldir/art/Lovely-889644244
And the little circles used for this are also shots from the same formula:
https://www.deviantart.com/rychveldir/art/Tribute-to-Benoit-B-Mandelbrot-905071991
A few days ago I simplified it a lot, so that instead of changing the formula between iterations, it just repeats the same iteration, then I use inside coloring. Here are a few examples of what it can do with the Julia version:



And here's a "Mandelbrot" version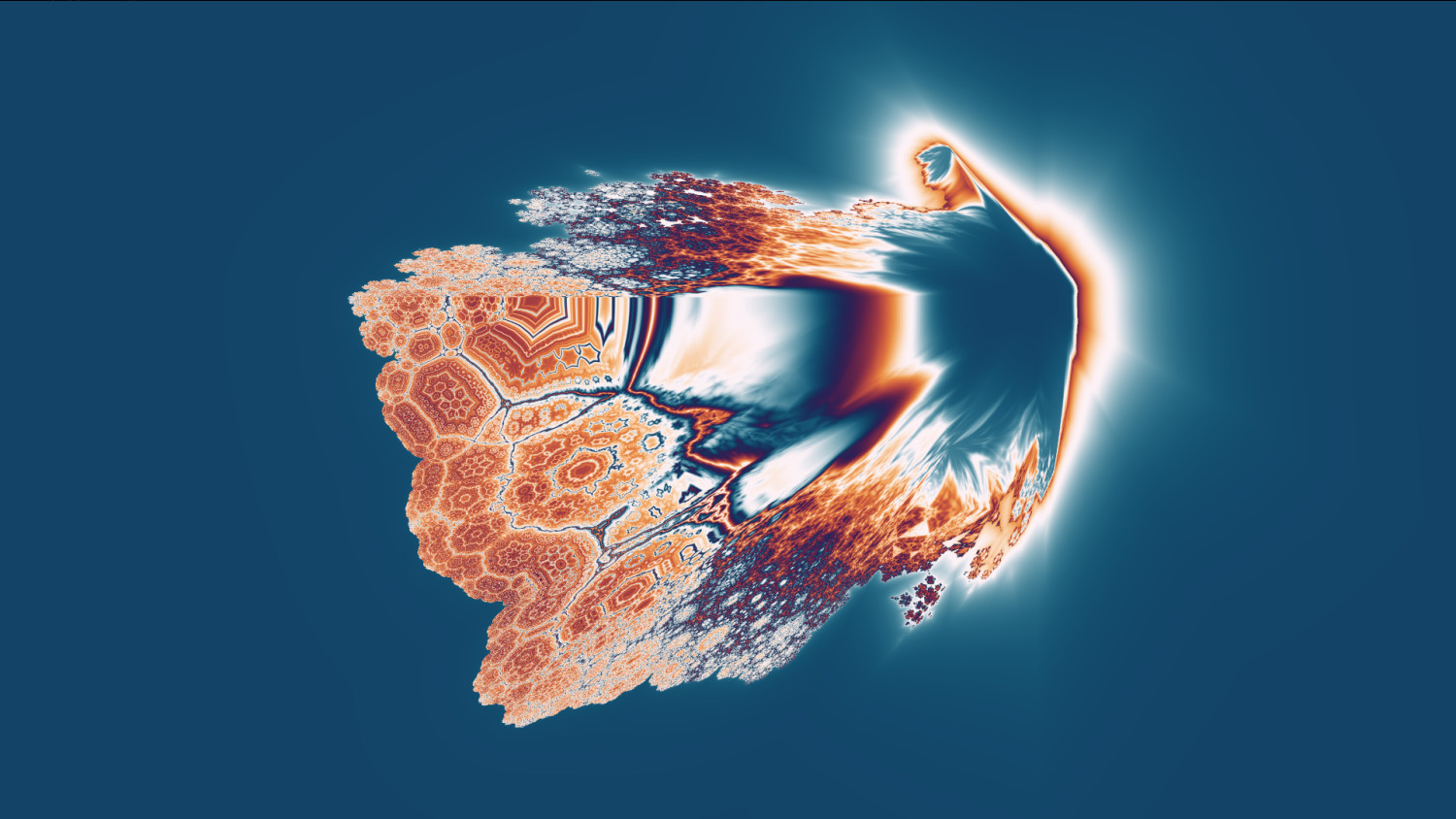
All these imgaes have a fairly low iteration count (in the high single or low double digits!), and none of them are deep zooms, so unlike my Coupling Loops, it's super fast as well. 
The iteration is fairly similar to the Burning Ship, except that I am using one exponent inside the abs function and then another outside of it: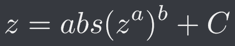
where a and b can be integers, float or even complex numbers. Generally the MB version looks distorted in many places, but the Julia Sets do not!
The current working title is burning_what2, but I need a better one before making it public!

